Краткий обзор результатов работ, выполненных различными исследователями
Срыв гидравлических затворов является следствием возникновения разрежений в канализационном стояке, поэтому прежде всего необходимо установить причины их возникновения, а также параметры, от которых зависит величина разрежений.
До настоящего времени не существует единой точки зрения относительно режимов течения сточной жидкости и .причин возникновения разрежений в канализационном стояке.
До 1970 г. рядом исследователей указывалось [22, 24], что течение сточной жидкости по стояку сопровождается периодическим образованием на отдельных его участках водяных «поршней», движущихся с большой скоростью и вызывающих резкие колебания давлений-В соответствии с этой точкой зрения величина разрежений зависит от скорости падающей жидкости, а скорость является функцией высоты стояка, критическое значение которой составляет 50 м. При падении жидкости с указанной высоты ее скорость достигает 4 м/с, что сопровождается возникновением разрежений критической величины, вызывающих срыв гидравлического затвора.
Такая скорость наблюдается в стояках высотой не более 50 м при следующих расходах: 2 л/с — для диаметра 50 мм; 9 л/с — для диаметра 100 мм; 20 л/с — для диаметра 150 мм [22]. В зданиях, в которых высота стояков превышает 50 м, рекомендуется устройство двухтрубной системы канализации. Конструктивная особенность двухтрубной системы заключается в устройстве вентиляционного стояка, присоединяемого через этаж перемычками к канализационному стояку.
Следует отметить, что данные работы [22] получены аналитически без учета затрат энергии жидкостью на эжекцию из атмосферы воздуха. В соответствии с исследованиями, проведенными в Ленинграде на стояках диаметрами 100 и 125 мм высотой 41 м [10], рекомендуется критическими расходами жидкости считать 4,4 л/с для стояка диаметром 100 мм и 6,98 л/с — для стояка диаметром 125 мм, что в 2 раза меньше нагрузок, рекомендуемых работой [22]. Более поздние экспериментальные исследования (табл. 4), выполненные за рубежом [31, 37], подтвердили данные работы [10].
Можно полагать, что величина эжектирующей способности зависит от параметров жидкости и воздуха и условий входа жидкости в стояк. Несоответствие между величиной эжектирующей способности жидкости и количеством воздуха, поступающим в стояк из атмосферы, приводит к образованию дефицита воздуха ниже сжатого сечения стояка (т. е. ниже водовоздушного поршня). Очевидно, что чем больше это несоответствие, тем больше величина разрежения в стояке.
Величина эжектирующей способности жидкости является функцией скорости ее движения. В соответствии с имеющимися экспериментальными данными скорость движения жидкости достигает максимального значения через 6—15 м падения. Отсюда можно заключить, что величина эжектирующей способности жидкости стабилизируется на этом же расстоянии от точки входа в стояк.
Величина разрежений в стояке является также функцией количества воздуха, поступающего из атмосферы через вытяжную часть стояка- Если вытяжная часть перестает функционировать (например, вследствие полного обмерзания), то стояк становится невентилируемым и его пропускная Способность уменьшается.
Аналитическое определение величины разрежений в канализационном стояке
Наличие эжектирующей способности у жидкости, движущейся в безнапорном режиме сверху вниз в вертикальном трубопроводе, можно объяснить взаимодействием жидкости и воздуха, которое является следствием молекулярного смачивания воздуха жидкостью, либо трением между ними; не исключается также наличие обоих факторов.
По данным канд.- техн. наук И. В. Мазюкевича, исследовавшего эжектирующие свойства поверхности стекающей жидкостной пленки, взаимодействие такой пленки с окружающей газообразной средой [15] зависит от скорости жидкости на поверхности пленки, величины поверхности пленки, а также разности плотностей газовой среды в пограничном слое и на некотором расстоянии от него.
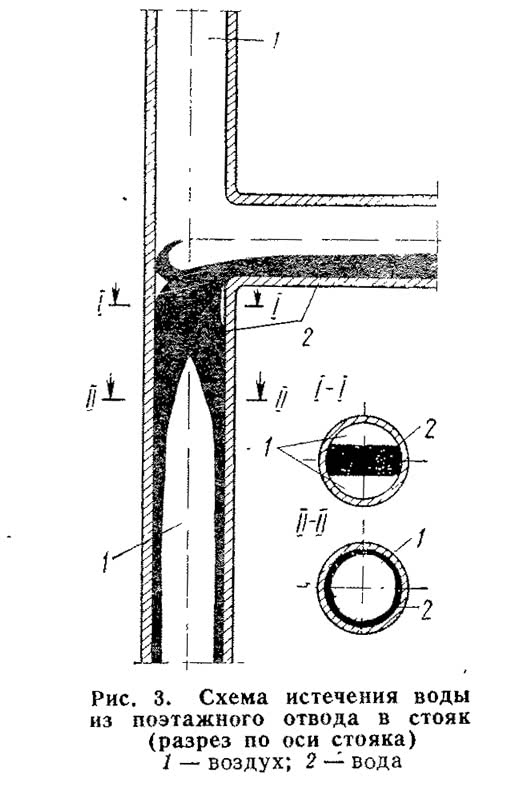
Рассмотрим механизм движения жидкости и воздуха в канализационном стояке на модели, представленной на рис. 3. Как уже установлено, сечение стояка на уровне присоединения отвода остается «сжатым» жидкостью до тех пор, пока не прекратится истечение жидкости из отвода. На некотором расстоянии от места входа происходит беспорядочное движение жидкости вниз по стояку. Затем жидкость попадает на стенки стояка и ее движение начинает стабилизироваться.
По данным Г. Рихтера [18], по мере движения жидкость прилипает к стенке трубопровода, что приводит сначала к образованию тонкого слоя, в котором скорость очень быстро снижается до нуля.
Известно, что при течении жидкости в круглой трубе постоянного диаметра (при полном заполнении) профиль скоростей движения имеет форму параболы с вершиной на оси трубы [1,2, 13, 29].
При стержневом» режиме течения в вертикальной трубе профиль скоростей движения жидкости, по-видимому, имеет вид параболы, не замкнутой на оси трубы, т. е. при неполном заполнении трубопровода ядро-течения жидкости отсутствует.
По данным Л. Шиллера [29], по мере продвижения жидкости (в горизонтальном трубопроводе с полным заполнением) ее пограничный слой вследствие трения утолщается и замедляет свое движение. На определенном расстоянии от входа в трубу, называемом начальным участком, пограничный слой захватывает все течение и эпюра скоростей принимает свою окончательную форму.
В вертикальной трубе с неполным заполнением в результате взаимодействия между жидкостью и воздухом на внешней поверхности жидкости образуется пограничный слой воздуха. Жидкость передает часть количества движения воздуху, вследствие чего воздух начинает двигаться в том же направлении, что и жидкость. При этом скорость воздуха является функцией скорости жидкости.
По данным Г. Шлихтинга [30], движение в пограничном слое остается ламинарным вплоть до значений числа Рейнольдса 5·105—106.
По данным И. К. Ротта [20], задача количественного расчета турбулентного пограничного слоя, образующегося на стенке при заданных условиях, на современном уровне знаний может решаться только полуэмпирическими методами.
При решении аналитической задачи о величине эжектирующей способности жидкости примем для простоты, что движение жидкости в стояке ламинарное и равномерное, т. е. силы инерции равны нулю. Примем также, что скорость движения частиц жидкости зависит только от» расстояния X по нормали к поверхности течения. Дифференциальное уравнение равновесия сил, действующих в стекающей пленке, в этом случае имеет вид:
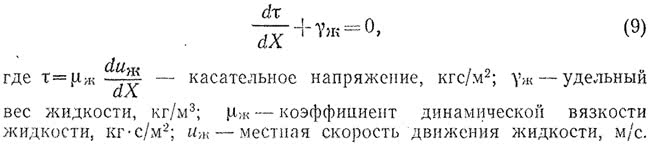
Интегрируя уравнение (9) при граничных условиях: при Х=0 uж=0 и при Х=?ж ?=0 — получим выражение, описывающее изменение скорости частиц в плоскости живого сечения пленки жидкости:
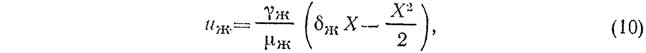
где ?ж — толщина пограничного слоя жидкости, м.
Скорость на внешней поверхности пленки при Х=?ж достигает максимального значения
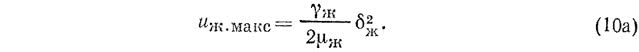
Средняя скорость движения жидкости в живом сечении пленки равна:
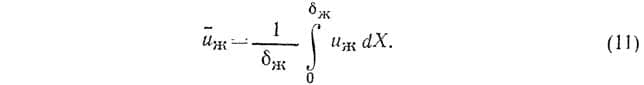
Используя выражение (10):
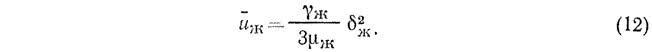
Из (10а) и (12):
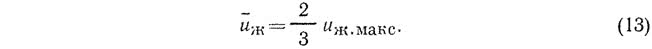
Объемный расход жидкости, м3/с, в пленке, стекающей по поверхности трубы (без учета ее кривизны), определяется уравнением
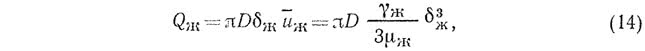
где D — диаметр трубы, м.
Отсюда толщина стекающей пленки
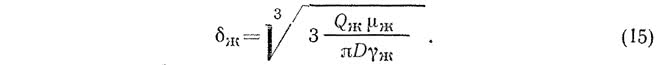
Из (12) и (15) средняя скорость движения в живом сечении пленки жидкости
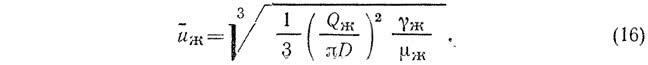
Скорость движения газового слоя на внешней границе стекающей жидкостной пленки в плоскости его живого сечения неодинакова и подчиняется сложной зависимости [15]. На границе раздела жидкости и газа скорость движения газа равйа скорости движения жидкости.
В первом приближении можно считать, что скорость движения газа изменяется линейно, т. е. величина касательных напряжений постоянна по ширине слоя.
Дифференциальное уравнение равновесия сил, действующих в газовом слое, имеет вид:
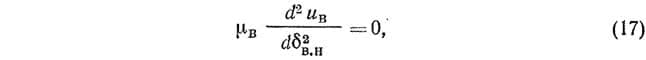
где ?в — коэффициент динамической вязкости воздуха, кг·с/м2; uв — местная скорость движения в газовом слое, м/с; ?в.н — расстояние (по нормали) от поверхности пленки в плоскости живого сечения газового слоя, м.
По данным канд. техн. наук И. В. Мазюкевича [15], местная скорость движения в газовом слое может быть определена из выражения:
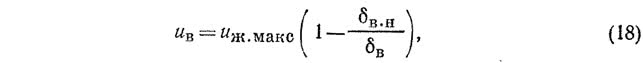
где ?в — толщина газового слоя, м.
Граничные условия: при ?в.н=0 uв=uж.макс, при ?в.н=?в uв=0.
Средняя скорость движения в плоскости живого сечения газового слоя
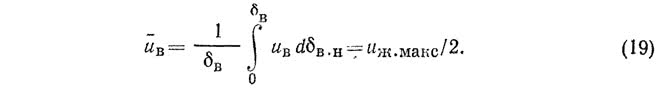
Таким образом, средняя скорость движения в плоскости живого сечения газового слоя является функцией максимальной скорости жидкости.
Выше отмечалось, что скорость жидкости достигает своего максимального значения в момент установления окончательной формы эпюры скоростей, т. е. в конце начального участка. По данным Л. Шиллера [29], окончательная форма эпюры скоростей устанавливается при значении
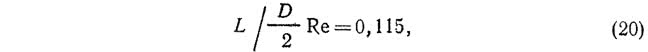
где L — длина начального участка, м; D — диаметр трубопровода, м; Re — число Рейнольдса.
Л. Шиллер рекомендует при турбулентном режиме принимать
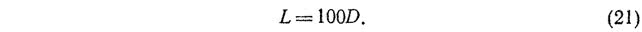
По данным Г. Рихтера [18], длина начального участка трубопровода круглого сечения определяется из выражения
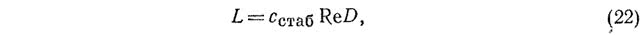
где сстаб — коэффициент стабилизации.
По данным Буссинеска [29], сстаб=0,065, откуда (при Re=1000) L/D=65.
По данным Г. Шлихтинга [30], при ламинарном режиме L=(100?200)D в зависимости от числа Рейнольдса.
Академик Б. Н. Юрьев рекомендует при определении длины начального участка пользоваться формулой
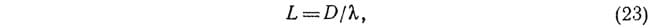
где ? — коэффициент сопротивления Дарси.
Все рекомендации по определению длины начального участка, приведенные выше, относятся к горизонтальным трубопроводам с полным заполнением. Аналогичных рекомендаций для опускного течения двухфазной смеси в вертикальной трубе в технической литературе не содержится. Однако несомненно, что и в интересующем нас случае длина начального участка является функцией диаметра трубы. Можно также предполагать, что в вертикальном трубопроводе течение стабилизируется раньше, чем в горизонтальном.
Поскольку от длины начального участка трубопровода зависит скорость движения жидкости, постольку от нее же зависит и скорость движения, а следовательно, и объемный расход эжектируемого воздуха. Отсюда следует, что с уменьшением (в пределах длины начального участка) высоты канализационного стояка связано также уменьшение величины эжектирующей способности жидкости; в то же время очевидно, что в канализационном стояке, высота которого равна длине начального участка или превышает ее, величина эжектирующей способности максимальна и постоянна.
Объемный расход воздуха, поступающего в стояк, может быть определен следующим образом:
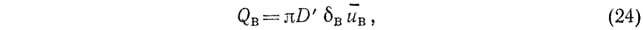
где D' — диаметр газового слоя по внешней поверхности пленки жидкости, м.
Очевидно, что в случае течения на плоской пластине толщина газового слоя не может быть определена однозначно, так как влияние трения в пограничном слое уменьшается по мере удаления от стенки асимптотически. Согласно данным Г. Шлихтинга [30], за толщину газового слоя принимается то расстояние от внешней границы жидкостной пленки, на котором скорость составляет 99% максимальной. При этом условии:
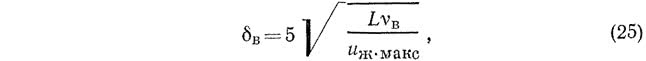
где 5 — коэффициент Блазиуса; vв — кинематическая вязкость воздуха, м2/с.
Пользуясь уравнениями (12), (16), (19) и (25), можно определить объемный расход, м3/с, воздуха, увлекаемого поверхностью жидкостной пленки:
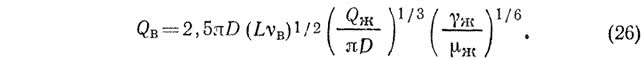
При выводе формулы (26) принято, что D'=D ввиду малого значения толщины жидкостной пленки по сравнению со значением диаметра трубы.
Последнее выражение дает возможность определить объемный расход воздуха, который движущаяся жидкость стремится увлечь за собой в стояк. Следует подчеркнуть, что такое количество воздуха поступало бы в стояк при отсутствии на пути воздуха гидравлических сопротивлений, т. е. величиной Qв характеризуется величина эжектирующей способности жидкости.
Однако в соответствии с принятой моделью течения на уровне присоединения поэтажного отвода к стояку на пути движения воздуха имеется местное гидравлическое сопротивление большой величины в виде водовоздушного поршня. В результате в стояк из атмосферы поступает количество воздуха, меньшее величины эжектирующей способности, что обусловливает возникновение дефицита воздуха (или разрежения) ниже сжатого поршнем сечения стояка.
Расход воздуха, м3/с, определяют по формуле
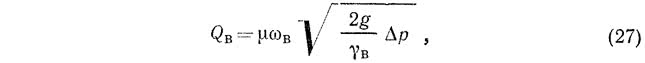
где ? — коэффициент расхода; ?в — площадь живого сечения воздуха в сжатом сечении стояка, м2 (см. рис. 3); g — ускорение свободного падения, м/с2; ?в — удельный вес воздуха, кг/м3; ?р — перепад давлений, кгс/м2.
Решая уравнения (26) и (27) совместно относительно ?р, имеем:
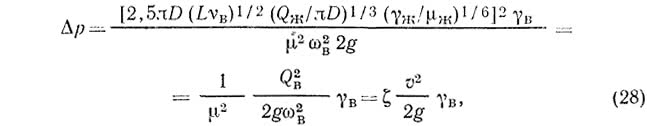
где ? — коэффициент местного сопротивления; v — скорость воздуха в сжатом сечении стояка, м/с.
Полученное выражение дает возможность проанализировать влияние основных параметров течения жидкости и воздуха на величину разрежений в канализационном стояке.
Величина разрежений увеличивается с ростом расхода жидкости. При увеличении расхода жидкости возрастает величина ее эжектирующей способности, площадь живого сечения воздуха в сжатом Сечении стояка сов уменьшается. При увеличении сов в 2 раза ?р уменьшается в 4 раза. Отсюда следует вывод о необходимости увеличения площади сечения воздуха в сжатом сечении стояка, что может быть достигнуто изменением условий входа жидкости в стояк, а именно уменьшением диаметра и угла присоединения к нему поэтажных трубопроводов.
Величина разрежений в стояке стремится к бесконечности при ?в?0, что может быть, например, при обмерзании вытяжной части стояка.
В то же время увеличение диаметра вытяжной части по сравнению с диаметром стояка малоэффективно, так как расход воздуха будет лимитироваться диаметром стояка.
Из формулы (28) следует, что величина разрежений достигает максимума в конце длины начального участка L. Дальнейшее увеличение высоты стояка не оказывает влияния на величину разрежения; уменьшение высоты стояка способствует повышению его пропускной способности.
С увеличением шероховатости материала трубопровода уменьшается длина начального участка (при прочих равных условиях) и, следовательно, уменьшается величина возникающих в стояке разрежений. Таким образом, пропускная способность стояка из шероховатых труб больше, чем из гладких. Поэтому нельзя подтвердить правильность существовавшего мнения о возможности замены чугунных канализационных труб диаметром 100 мм с коэффициентом шероховатости 0,013 полиэтиленовыми диаметром 75 мм с коэффициентом шероховатости 0,01.
Величина эжектирующей способности жидкости — числитель формулы (28) — увеличивается с увеличением диаметра стояка. Тот факт, что стояк большего диаметра имеет все же большую пропускную способность, объясняется существенным уменьшением площади живого сечения воздуха в сжатом сечении стояка большего диаметра при одинаковом расходе жидкости. Кроме того, следует отметить, что изменение удельного веса жидкости практически весьма невелико. С повышением температуры стоков величина разрежений в стояке несколько уменьшается.
Наличие компонентов твердой фазы в сточной жидкости не оказывает практического влияния на пропускную способность стояка. Так, по данным Н. Ф. Федорова [25], удельный вес бытовых сточных вод практически не отличается от удельного веса чистой воды. По данным М. В. Мальцева, гидравлические потери при движении трехфазных смесей (вода + воздух + твердое) в вертикальных трубах определяются потерями, обусловленными движением жидкой фазы [16]. Этот вывод значительно облегчает проведение экспериментальных исследований, освобождая от необходимости моделировать сточную жидкость.
Анализ выражения (28) также показывает, что изменение параметров воздуха незначительно влияет на величину разрежений в канализационном стояке и при расчете ими можно пренебречь (в числитель указанного выражения кинематическая вязкость vв и удельный вес воздуха ?в входят в первой степени и изменяются обратно пропорционально).
Следует, однако, указать, что расчет по формуле (28) осложняется из-за отсутствия данных о величине площади живого сечения воздуха в сжатом сечении стояка сов, неизвестна также величина коэффициента расхода р. Кроме того, формулой (28) не учитываются условия входа жидкости в стояк. Следовательно, расчет надземной части систем канализации зданий должен базироваться на экспериментальных исследованиях.