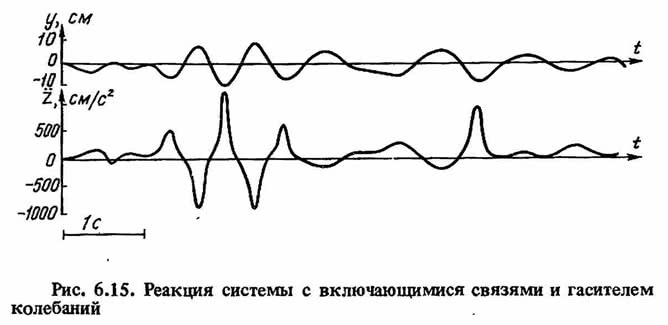
Реакция системы с включающимися связями и динамическим гасителем

Реакция системы с включающимися связями и динамическим гасителем колебаний при сейсмических воздействиях.

В гл. 3 дано представление о системах с включающимися связями, указана область возможного их применения в сейсмостойком строительстве, отмечены достоинства и недостатки этой системы.

Колебания таких систем, имеющих билинейную жесткост-ную характеристику при воздействиях типа сейсмических, исследовались в работах [2, 138]. Система с включающимися связями, имеющая более сложную жесткостную характеристику, получаемую за счет многоступенчатости включения связей, исследовалась при модельных испытаниях на сейсмоплатформе [75].

Применение включающихся связей, приводящих к изменению жесткости сооружения по мере увеличения интенсивности нагрузки, позволяет ограничить перемещения сооружения необходимым уровнем при любом типе землетрясений. Однако при землетрясениях, имеющих широкий спектральный состав колебаний грунта в системе, возможно многократное включение связей и возникновение значительных усилий в конструкциях включающихся связей. Эти усилия можно существенно уменьшить в случае совместного применения системы с включающимися связями и динамическим гасителем колебаний. Ниже дан анализ работы такой комбинированной системы сейсмозащиты и приведены результаты модельных испытаний на сейсмоплатформе.

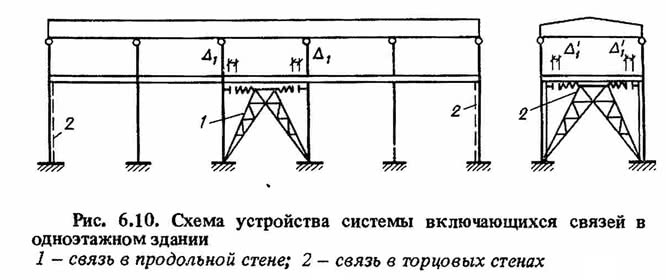
Рассмотрим работу системы с включающимися связями при реальном землетрясении на примере одноэтажного каркасного здания (рис. 6.10). В состоянии покоя между связями, жестко закрепленными на порталах (или панелях заполнения), и рамой каркаса, имеется зазор.

При воздействии на здание сейсмического толчка, характеризующегося преобладанием высокочастотной части спектра, панели заполнения, отделенные зазором от каркаса, до момента закрытия зазоров не будут оказывать влияния на жесткостные характеристики здания. При таких колебаниях здание будет оставаться гибким и будет иметь период собственных колебаний, далекий от доминантных периодов колебаний грунта. Это позволяет избежать резонансных колебаний здания, при которых сейсмическая реакция конструкции сильно возрастает.

При воздействии на здание землетрясения, характеризующегося преобладанием колебаний в области низких частот, каркас здания получит перемещения, превышающие зазор ?₁. В этом случае имеющиеся связи включают в работу порталы, панели заполнения или другие аналогичные конструкции, которые, значительно увеличивая жесткость всей конструкции здания, изменяют его период собственных колебаний в сторону уменьшения, в результате чего здание "уходит" от опасных для него резонансных колебаний.

Такой характер поведения системы с включающимися связями может быть проиллюстрирован результатом расчета на АВМ системы с билинейной характеристикой, имеющей период собственных колебаний основной конструкции (каркаса здания) Т₀ = 1,2 с, затухание в системе 5% критического, отношение коэффициента жесткости системы с включенными связями к коэффициенту жесткости основной конструкции системы, равное 4 и зазор ?, равный 4,2 см, на воздействие, соответствующее записи Карпатского землетрясения 4 марта 1977 г. (компонента север-юг). Результаты расчета в виде записей полного ускорения и относительного смещения системы с включающимися связями (1) приведены на рис. 6.11. Там же для сравнения приведены результаты расчета для обычной системы с одной степенью свободы (2). На записи ускорения системы хорошо видны моменты включения связей. После четырех включений связей система вышла из резонансного режима колебаний. По сравнению с колебаниями системы с одной степенью свободы максимальное относительное смещение уменьшилось в 3,4 раза.

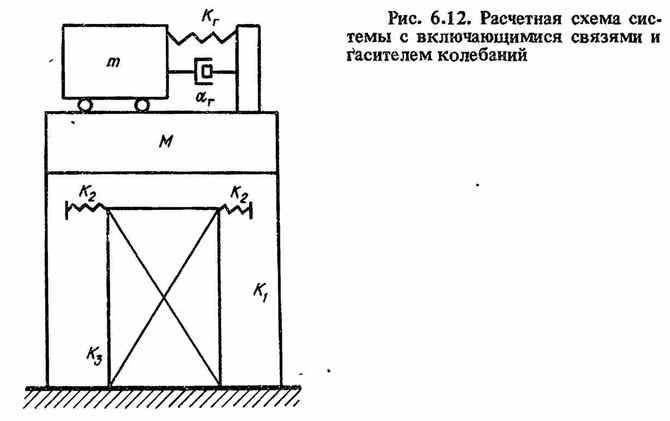
Рассмотрим колебания системы с включающимися связями и гасителем колебаний (рис. 6.12) при движении основания по закону у₀. Дифференциальные уравнения движения главной массы и гасителя имеют вид:

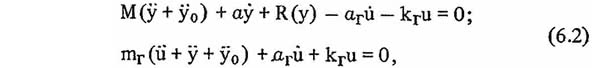
где y — смещение главной массы относительно основания; u - смещение массы гасителя относительно главной массы; R(y) - нелинейная восстанавливающаяся сила в основной системе.

Частота свободных колебаний нелинейной, системы зависит от ее амплитуд. Поэтому колебания нелинейной системы приближенно можно представить колебаниями линейной системы с собственной частотой, зависящей от амплитуды. Тогда систему уравнений (6.2) можно записать в следующем виде:

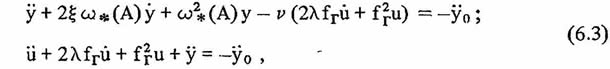
где ?*(А) - мгновенная частота свободных колебаний нелинейной системы; f_г - частота свободных колебаний массы гасителя; ? и ? - безразмерные коэффициенты вязкости для главной массы и массы гасителя; v = m/M - относительная масса гасителя.

Зависимость мгновенной частоты собственных колебаний ?*(А) от амплитуды колебаний может быть получена одним из методов, применяемых в теории нелинейных колебаний, например, методом припасовывания.

Считая, что зависимость ?*(А) известна, рассмотрим решение системы (6.3) для случая движения основания по гармоническому закону с частотой р₀ и амплитудой а₀. Будем решение уравнений (6.3) искать в следующем виде:

Подставив выражения (6.4) в систему (6.3) и перейдя после ряда преобразований от комплексной формы записи к действительной, а также введя следующие обозначения:

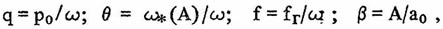
получим


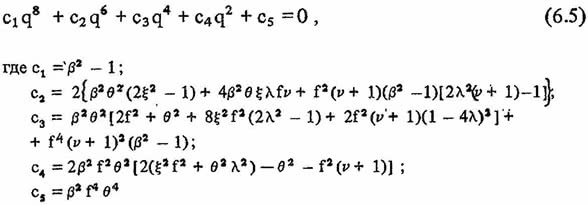
Решая уравнение (6.5) Относительно q², получим

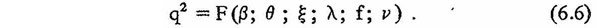
Задаваясь значениями ? при постоянных смещениях основания а о и параметрах гасителя ? и f, можно построить зависимость q от величины ?, называемой амплитудно-частотной характеристикой нелинейной системы.

Приняв в выражениях для коэффициентов уравнения (6.5) ? = f = v = 0, подставим их значения в (6.5) и, решая относительно q², получим для системы без гасителя

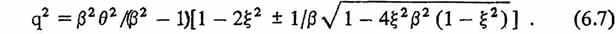
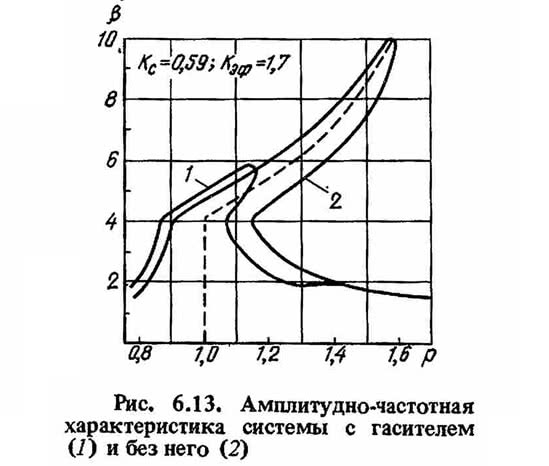
В качестве примера рассмотрим амплитудно-частотные характеристики системы с билинейной характеристикой с гасителем и без него. Параметры системы приняты следующие: соотношение коэффициентов жесткости k₂/k₁ = 4; ? = 0,05; ?/а₀ = 4; f = 1,3; ? = 0,1; v = 0,05.

Для построения скелетной кривой системы, определяющей ?*(А), воспользуемся известным решением для билинейной системы, приведенным, например в [6]. Тогда формулу для определения ?*(А) можно записать в следующем виде:

Скелетная кривая системы с вышеуказанными параметрами приведена на рис. 6.13 (пунктирная линия). Там же приведены амплитудно-частотные характеристики системы с гасителем (1) и без него (2). Для системы с гасителем максимальное значение характеристики меньше соответствующего значения для системы без гасителя в 1,7 раза. Кроме того, в системе с гасителем ширина резонансной зоны меньше, чем в системе без гасителя, что имеет положительное значение при полигармоническом движении основания.

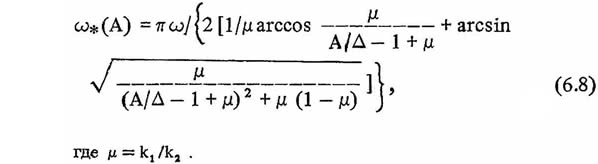
Выбор параметров системы с включающимися связями и гасителями колебаний должен производиться на основе расчета по ансамблю реализаций расчетного землетрясения. Здесь в качестве примера приведем результат расчета, выполненного по записи Газлийского землетрясения 17 мая 1976 г. (компонента север-юг), имеющего широкополосный спектр. Задача о колебаниях системы решалась на АВМ.

Была рассмотрена система, имеющая период собственных колебаний основной конструкции, равный 1,1 с, отношение коэффициента жесткости системы с включенными связями к коэффициенту основной системы, равное 4, зазор между связями, равный 8 см,и относительную массу гасителя, равную 0,05. Частота гасителя и затухание в гасителе оптимизировались в процессе расчета, исходя из условия минимума среднеквадратического значения амплитуд полного ускорения системы.

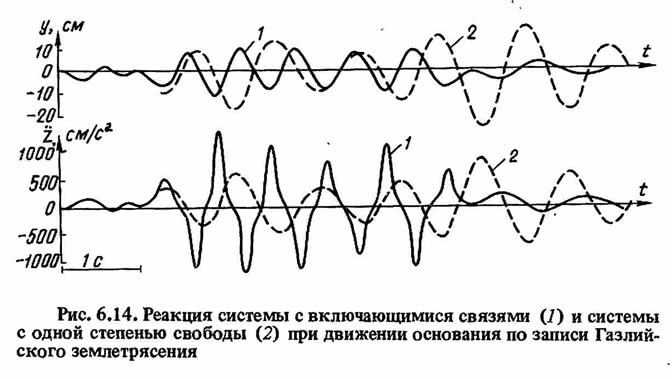
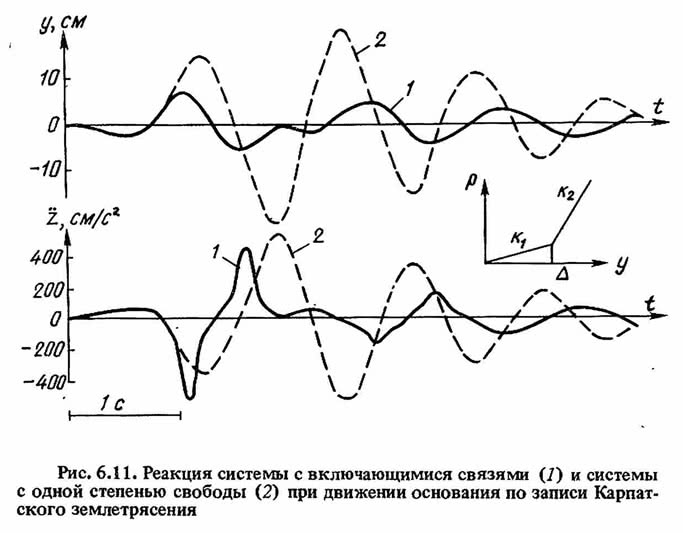
Для проведения сравнительного анализа были рассчитаны система с включающимися связями без гасителя и линейная система с одной степенью свободы. Результаты расчета в виде записей полного ускорения и относительного смещения этих систем приведены на рис. 6.14. В системе с включающимися связями (7) максимальное относительное смещение уменьшилось в два раза по сравнению с максимальным смещением системы с одной степенью свободы (2). При этом максимальное ускорение системы с включающимися связями возросло в 1,72 раза.

На рис. 6.15 приведены записи полного ускорения и относительного смещения системы с включающимися связями и гасителем колебаний со следующими параметрами: отношение частоты гасителя к частоте собственных колебаний основной системы равно 1,30 и затухание в гасителе составляет 9% критического. Такая настройка и затухание в гасителе оказались оптимальными. В системе с гасителем максимальное ускорение и максимальное смещение системы с включающимися связями снизилось на 10%, среднеквадратическое значение амплитуд ускорения системы на 35% и среднеквадратическое значение амплитуд смещения на 20%. Число включения связей уменьшилось с 11 до 6 раз. Установлено, что изменение настройки гасителя в пределах 10% мало влияет на эффективность гашения колебаний.