Расчет составных стержней на продольный изгиб

Устойчивость составного сжатого стержня проверяют по общей формуле

в которой коэффициент продольного изгиба ?_у определяется по приведенной гибкости ?_пр, учитывающей податливость соединений и конструктивные особенности составного стержня при расчете его относительно оси у, параллельной швам сплачивания (рис. 76). Приведенная гибкость в общем случае выражается формулой

здесь ?_у — гибкость всего элемента относительно оси у, определенная по расчетной длине элемента l₀ без учета податливости соединений;
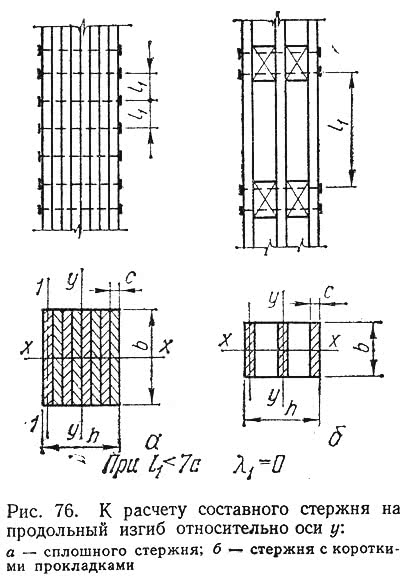
?₁ — гибкость отдельной ветви относительно ее оси 1—1, вычисленная по расчетной длине ветви l₁, при l₁ меньше семи толщин ветви (l₁ ?_y — коэффициент приведения гибкости составного стержня, учитывающий податливость связей,

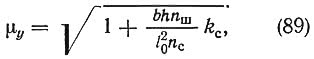
где b и h — полная ширина и высота сечения элемента, см;
n_ш — число рабочих швов в элементах, по которым суммируются взаимные сдвиги ветвей;
l₀ — расчетная длина элемента, м;
n_с — расчетное число срезов в одном шве на 1 м длины элемента (при нескольких швах с различным числом срезов принимается среднее для всех швов число срезов);
k_с — коэффициент податливости соединений, определяемый по табл. 2 приложения 9.

Наиболее распространены четыре типа сжатых составных стержней (рис. 77):

1. Стержни-пакеты, состоящие из ветвей равной длины, вплотную прилегающих друг к другу (рис. 77, а). Расстояние между связями в таких стержнях обычно l₁1 = 0. Относительно оси х стержень рассчитывается как цельный.

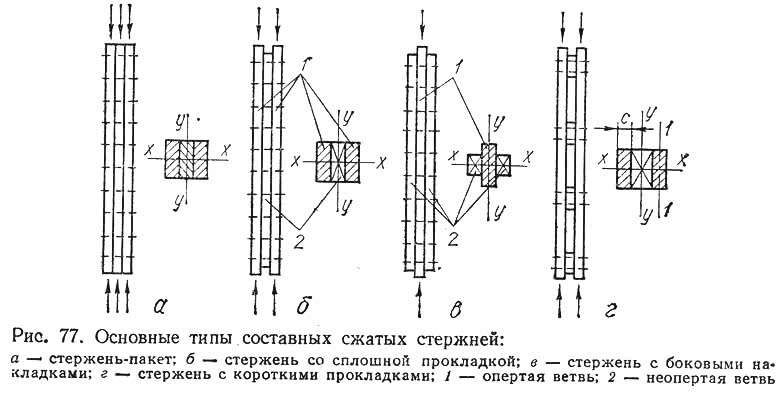
2. Стержни со сплошными прокладками, состоящие из ветвей, разделенных длинными прокладками почти на всю длину стержня (рис. 77, б). Как и в первом случае при ?₁ = 0 приведенная гибкость ?_пр = ?_y?_y. Основные ветви доходят до опоры и воспринимают нагрузку непосредственно, а прокладки до конца не доходят и воспринимают нагрузки через связи (неопертые ветви). При расчете относительно оси у расчетные моменты инерции определяются с учетом всех ветвей (опертых и неопертых): I_y = I_о + I_н.о. При расчете относительно оси х расчетный момент инерции I_x = I_о + 0,5 I_н.о.

Расчетная площадь поперечного сечения равна сечению только опертых ветвей (F = F_о).

Расчетный радиус инерции и гибкость относительно оси у:

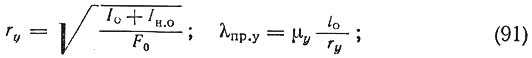
то же, относительно оси х:

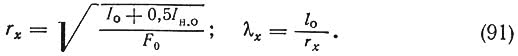
3. Стержни с боковыми накладками, расположенными почти по всей длине (рис. 77, в). Накладки нужны для увеличения жесткости элемента относительно оси у. Расчет таких стержней производится по тем же формулам, что и стержней со сплошными прокладками.

4. Стержни с коротк ими прокладками (рис. 77, а), расположенными на некотором расстоянии друг от друга, которое обычно не превышает 7с, где с — наименьший размер сечения ветви. Приведенная гибкость стержня определяется по формуле (88), расчетная длина ветви принимается равной расстоянию l₁ между крайними связями прокладок.

При проектировании составных стержней, расчет которых ведется с учетом гибкости отдельной ветви, длину ветви необходимо назначать из условия, чтобы ее гибкость не превышала гибкости всего стержня, т. е. l₁??_y?_yr₁.