Расчет элементов работающих на сложное сопротивление

К элементам, работающим на сложное сопротивление, относятся элементы, которые находятся одновременно под воздействием продольной силы N и изгибающего момента М. Сложное сопротивление элементов вызывается следующими усилиями (рис. 42): внедентренным действием продольной силы; совместным действием продольной силы и нагрузки, вызывающей поперечный изгиб; продольной силой при кривизне элемента (например, для верхних поясов ферм с сегментным очертанием); продольной силой при несимметричном ослаблении поперечного сечения элемента.

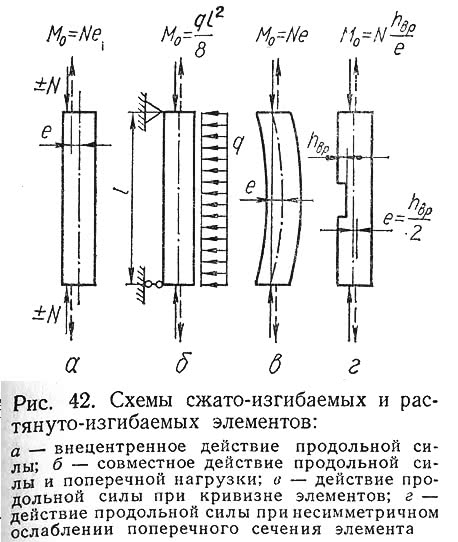
В зависимости от знака продольного усилия различают сложное сопротивление сжатию с изгибом и сложное сопротивление растяжению с изгибом. Верхние пояса балочных ферм при наличии на панелях местной поперечной нагрузки или при наличии несимметричных ослаблений, вызванных конструкцией узлов, являются сжато-изгибаемыми элементами. Нижние пояса ферм при тех же условиях будут растянуто-изгибаемыми. К сжато-изгибаемым элементам относятся стойки (колонны) каркасов зданий, нагруженные продольными вертикальными и поперечными нагрузками от действия ветра.

Сжато-изгибаемые элементы относятся ко II, а растянуто-изгибаемые к I категории элементов деревянных конструкций. В деревянных конструкциях рекомендуется по возможности избегать применения растянуто-изгибаемых элементов, наиболее чувствительных к порокам и к местным ослаблениям сечений врубками и отверстиями.

Предельное состояние элемента при сложном сопротивлении с учетом различной прочности материала на сжатие и изгиб выражается формулой

В этой формуле F_нт, W_нт — площадь и момент сопротивления нетто рассчитываемого сечения;
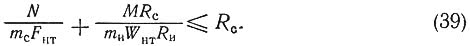
R_с, R_н — расчетные сопротивления сжатию вдоль волокон и изгибу;
N, М — расчетные усилия в рассматриваемом сечении.

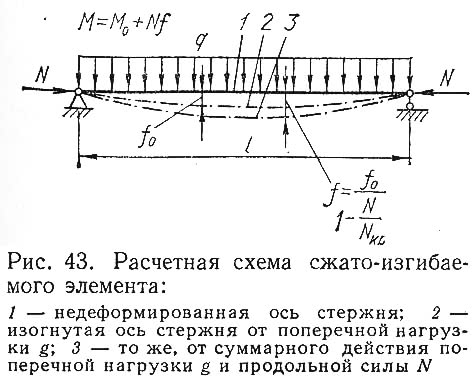
По расчетной схеме (рис. 43) находим, что расчетный изгибающий момент М состоит из двух частей:

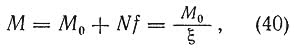
где М₀ — момент от поперечной нагрузки или внецентренно приложенной продольной силы, по недеформированной схеме, не зависящий от прогиба;
Nf — момент от продольной силы N по деформированной схеме, зависящий от прогиба f, т. е. дополнительный момент; этот момент учитывается коэффициентом ?, который находится по формуле

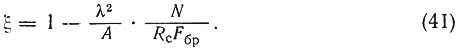
Значения величин A/?² для различных конструкционных материалов приведены в табл. 9.

Окончательно формула для проверки прочности сечения при сложном сопротивлении сжатию с изгибом принимает вид:

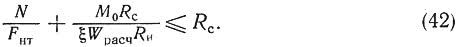
Огержни с малыми гибкостями (при ?мин), когда напряжения изгиба ?_и = M₀/W_нт не превышают 10% напряжений сжатия ?_с = N/F_нт, следует рассчитывать только на устойчивость по формуле (16) без учета изгибающего момента.

Кроме расчета на прочность в плоскости изгиба сжато-изгибаемые элементы должны быть проверены на устойчивость из плоскости изгиба от действия одной продольной силы N по формуле (16).

Расчетные значения поперечной силы Q и сдвигающего усилия Т в сжато-изгибаемых элементах находятся по формулам:

Здесь Q₀ и I₀ — поперечная сила и сдвигающее усилие только от поперечной нагрузки.

Проверка на скалывающие напряжения производится по формуле (33).

Прогибы сжато-изгибаемых элементов вычисляют исходя из формул для изгибаемых элементов, но с учетом увеличения их от совместного действия сжатия с изгибом:

где f₀ — прогиб, который находится только от поперечной нагрузки.

Учет влияния сдвигающих напряжений на прогиб производится, как для изгибаемых элементов по формуле (36).

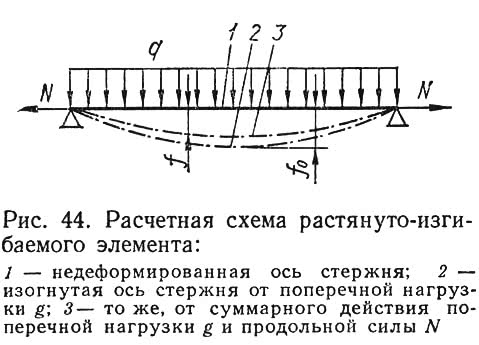
При расчете растянуто-изгибаемых элементов на растяжение с изгибом влиянием прогиба стержня от поперечной нагрузки пренебрегают, так йак возникающий при этом дополнительный момент приводит к уменьшению момента от поперечной нагрузки (рис. 44). Сечение проверяют по формуле