Проблема аэродинамической устойчивости сооружений, т. е. регулярных колебаний при ветре, привлекает все большее внимание проектировщиков строительных конструкций. При ветре наиболее часто наблюдаются вибрации проводов, стальных канатов, труб различного назначения, элементов трубчатых конструкций, висячих мостов, радиомачт. Для возбуждения и поддержания многих видов колебаний достаточна скорость ветра до 10 м/сек, т. е. наблюдаемая не так редко. Скорость ветра около 20 м/сек способна заставить колебаться крупные сооружения и большепролетные висячие мосты.
Причиной вибрации конструкций при ветре является прежде всего их форма, рассматриваемая с позиций аэродинамической устойчивости тела в потоке жидкости. Это условие необходимо, но недостаточно, так как размеры и жесткость сооружения, рассеяние энергии в нем могут не допустить появления регулярных колебаний. Аэродинамически неустойчивая форма требует более детального исследования поведения конструкции с привлечением опытов в аэродинамической трубе и водяном канале, потому что такие колебания приводят к преждевременному выходу из работы деталей и даже к обрушению сооружения.
Наиболее интересно поведение упругого круглого цилиндра в потоке воздуха, потому что трубы и трубчатые конструкции, получающие все большее распространение, наиболее часто подвержены вибрации.
Предварительно рассмотрим поведение неподвижного круглого цилиндра в потоке жидкости. При обтекании у его противоположных сторон образуются поочередно вихри правого и левого вращения, которые затем срываются и движутся со скоростью, немного меньшей, чем скорость потока на бесконечности (см. рис. 3.13).
Частота срывов вихрей с жестко закрепленного круглого цилиндра в большом интервале чисел Рейнольдса определяется числом Струхаля
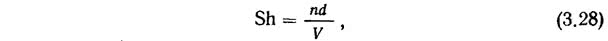
равным 0,2 для всех чисел Рейнольдса, за исключением интервала очень малых чисел.
В области кризиса обтекания числа Струхаля дают разброс, достигая значений 0,45 и 0,1. За кризисом Sh?0,2. Это установлено косвенными приемами: по замеренной частоте и скорости потока, обтекающего цилиндры большого диаметра (например, у дымовых труб), по снежным и песчаным вихрям, наблюдаемым за самодвижущимся экипажем (автомобиль, поезд), а также по ритмичным ударам по румпелю движущейся яхты. Такие вихри хорошо заметны за быками речных мостов. Эти примеры свидетельствуют о регулярных срывах вихрей при числах Рейнольдса 107 и более.
Срывы вихрей наблюдаются у разнообразных по профилю тел; частота срывов определяется числом Струхаля, значение которого колеблется в широких пределах, от 0,12 до 0,65 (см. табл. 3.1 и 3.5) и шире. Разные значения чисел Струхаля зависят от того, что принимается в формуле (3.28) за размер d: ширина дорожки вихрей или характерный, т. е. поперечный к потоку, размер тела. Причиной разброса чисел Струхаля могут быть способы оценки частоты.
Вихри, срывающиеся с цилиндра с частотой, определяемой числом Струхаля, приводят к появлению знакопеременной подъемной силы. Механизм этого явления заключается в следующем: при срыве вихря, например, с нижней стороны горизонтального цилиндра (левое вращение), возникает вращательное движение жидкости, противоположное по знаку вращению оторвавшегося вихря, что следует из постоянства циркуляции (теорема Томсона). Это вращательное движение жидкости вокруг цилиндра приводит к увеличению скорости сверху и к ее понижению снизу, что по теореме Бернулли повышает давление снизу цилиндра и понижает — сверху. Вследствие разности давлений возникает направленная поперек потока и вверх подъемная сила. Через полупериод, определяемый для круглого цилиндра числом Струхаля, равным 0,2, срывается сверху вихрь правого вращения; циркуляция будет противоположного вращения, что вызывает появление подъемной силы, направленной вниз. Через следующий полупериод картина зеркально повторится и т. д. При неизменной скорости потока такие вихри регулярно срываются с цилиндра и на него также регулярно действуют импульсы силы. Подъемная сила не может мгновенно появиться и исчезнуть через полупериод, что объясняется инерцией жидкости, поэтому график движения ее имеет вид синусоиды со сдвигом фазы приблизительно на 90° относительно движения. Это установлено опытами в трубе с использованием градуированных датчиков давления с поправками на инерцию [24].
При изучении- периодических явлений требуется не только геометрическое подобие модели и равенство чисел Рейнольдса, но и уравнивание чисел Струхаля.
Механизм движения упруго закрепленного круглого цилиндра в потоке жидкости сложнее, но вместе с тем имеется много общего с обтеканием неподвижного цилиндра. При отрыве вихря с цилиндра также возникает подъемная сила, заставляющая его перемещаться в направлении поперек потока до тех пор, пока не установится равновесие. После этого цилиндр под влиянием восстанавливающей силы (пружины, упругости материала) начнет двигаться в противоположном направлении. Если скорость потока такова, что через промежуток, равный полупериоду колебаний цилиндра, сорвется вихрь с другой стороны, т. е. противоположного вращения, то возникнет подъемная сила обратного знака, стимулирующая начавшееся под влиянием восстанавливающей силы движение. Через полупериод, также определяемый числом Струхаля, равным 0,2, снова возникает из-за срыва вихря подъемная сила, которая также будет поддерживать возникшие поперечные к потоку колебания.
В отсутствии рассеяния энергии амплитуда колебаний возросла бы до бесконечности. В реальных условиях потери энергии в системе «цилиндр — окружающая среда», растущие с амплитудой колебании, становятся, наконец, равными подводимой из потока энергии, если до этого не произойдет разрушение материала цилиндр а, ил и его опорных закреплений. После этого колебания будут происходить с постоянной амплитудой и неизменной частотой. Они называются самовозбуждающимися колебаниями или автоколебаниями, потому что поток, из которого черпается энергия, не обладает, периодическими свойствами. Механизмом обратной связи в трактовке теории колебаний являются срывающиеся с цилиндра вихри, в силу чего происходит периодическое заимствование из потока энергии для восполнения потерь в колеблющейся системе.
Срывы вихрей с цилиндра происходят в его крайних положениях или вблизи их. Очень важно, что срыв вихрей наблюдается одновременно по всей длине цилиндра. Если колебания цилиндра происходят с несколькими полуволнами, то вихри срываются в крайних положениях одновременно с каждой полуволны. Это установлено визуализацией течения вокруг цилиндра с помощью пузырьков газа, образующегося при электролизе воды в канале. Исследуемый цилиндр служил одним из электродов.
Величина подъемной силы у колеблющегося цилиндра определялась рядом исследователей в разнообразных по постановке опытах, а также теоретическим путем. Значения коэффициента подъемной силы су оказались в широких пределах (от 0,1 до 1,5), что объясняется разными условиями экспериментов или гипотезами в основе теоретических расчетов. При проверке на «резонанс» цилиндрических конструкций по СНиП принимают коэффициент су=0,3.
Колебания упругих цилиндров в потоке происходят приблизительно с собственной частотой; они начинаются, когда число Струхаля приближается к 0,2. С повышением скорости потока частота колебаний гибкого цилиндра незначительно растет, затем они срываются и возобновляются на частоте следующей гармоники. В опытах с гибкими стержнями удалось наблюдать три формы колебаний: с частотами 3,5; 22 и 61,7 гц, что соответствует гармоникам однородного консольного стержня (МГУ).
Затягивание колебаний цилиндров, замеченное до 3V, где V — скорость потока, определяемая числом Sh=0,2, может быть даже и при больших величинах V. Это неоднократно наблюдалось на проводах высоковольтных линий электропередачи, что также свидетельствует о самовозбуждающихся колебаниях, а не о резонансе в обычном понимании. Затягивание колебаний зафиксированы и при снижении скорости потока.
Колебания, вызываемые периодическим срывом вихрей, наблюдаются у различных по форме поперечного сечения цилиндров-стержней.
Вибрация круглых цилиндров замечена при скоростях ветра от долей метра до 15—20 м/сек, т. е. она наблюдается довольно часто, если цилиндры расположены на большой высоте от поверхности земли. Опасной областью такого рода колебаний круглых стальных стержней решетчатых конструкций будут элементы с гибкостью от 100 до 350.
Вибрацию стержней гасят с помощью подвесок, узловых закреплений или других конструктивных приемов, которые можно назвать пассивными. Активный прием гашения вибрации цилиндров — аэродинамический, когда воздействуют на характер обтекания таким образом, чтобы не возникала регулярная подъемная сила, возбуждающая колебания.
Картина обтекания круглого цилиндра определяется в основном местом отрыва пограничного слоя, толщина которого мала. Это открывает путь управления им с помощью устанавливаемых на цилиндре небольших по высоте препятствий — интерцепторов, так как не следует увеличивать сильно ветровую нагрузку. Наилучшее действие на вертикальные цилиндры оказывают спиральные (винтовые) интерцепторы. Кроме того, они на меньшую величину повышают сопротивление цилиндра ветру (см. рис. 3.28).
Для горизонтального цилиндра достаточно интерцептора под утлом 0°. Интерцепторы оказались эффективным средством гашения вибрации висячих трубопроводов, стальных дымовых труб, телевизионной башни высотой 180 м, телевизионной трубчатой мачты высотой 301 м и др. [25].
Интерцепторы по образующим цилиндра гасят или стимулируют колебания в зависимости от угла их установки. Например, интерцептор под углом около 45° к передней критической точке стимулирует колебания (см. рис. 3.29), установка другого под углом —45° увеличивает неустойчивость цилиндра. Спиральные интерцепторы свободны от такого недостатка, поэтому им следует отдавать предпочтение при гашении вибрации вертикальных цилиндров.
На графике нодъемной силы су (см. рис. 3.29) видно, что в окрестности угла ?=45° производная дcy/д?
Перфорация трубы или «рубашка» из перфорированного цилиндра гасит вибрацию трубы.
Более опасны колебания неизолированного цилиндра, т. е. расположенного, например, в аэродинамическом следе (в кильватерной струе) другого или где есть параллельные ему другие цилиндры. Срывы вихрей с переднего по потоку цилиндра, сильная турбулизация способствуют аэродинамической неустойчивости заднего.-Вибрация неизолированных тел возникает значительно легче — при меньшей скорости потока — и может поддерживаться в широком диапазоне скоростей, а не в определенном интервале их, поэтому она более опасна [26].
Вибрация парных канатов, параллельных трубопроводов, труб тепловых Электростанций, антенн с трубчатыми вибраторами, проводов линий электропередачи с расщепленной фазой и др. — наиболее частые примеры таких колебаний.
Одним из простых приемов гашения вибрации параллельных стержней и гибких нитей (провода, канаты) с одинаковым электрическим потенциалом служит взаимное раскрепление их по методу «узел — пучность — узел», т. е. механическое соединение узла колебаний одного стержня с пучностью соседнего [25].
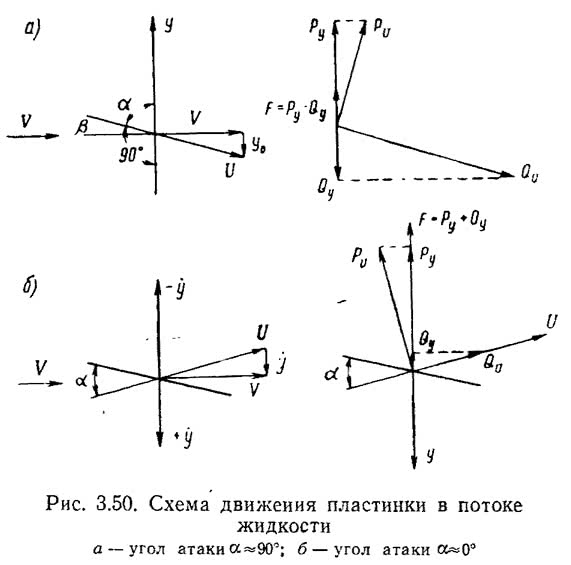
Механизм поперечных колебаний пластинки заключается в следующем: скорость движения ее при малых значениях перемещения может быть выражена через угол а. Тогда графики подъемной силы и составляющей лобового сопротивления в функции угла атаки (см. рис. 3.7) будут характеризовать силы, воздействующие на пластинку. Подъемная сила, имеющая отрицательный наклон в окрестности угла ?=90°, стимулирует колебания. Составляющая лобового сопротивления на направление движения также будет способствовать развитию колебаний, поскольку коэффициент сх уменьшается с увеличением или уменьшением угла ?=90°—?. Движение пластинки будет происходить до наступления равновесия, определяемого восстанавливающей силой. После этого под влиянием этой силы пластинка начнет двигаться в противоположном направлении, чему будут способствовать подъемная сила и составляющая лобового сопротивления. В другом крайнем положении опять наступит равновесие, затем начнется движение в обратном направлении и т. д. Амплитуда колебаний пластинки будет расти до тех пор, пока подводимая за период энергия из потока не станет равной рассеяннной в системе. После этого установятся незатухающие колебания, т. е. колебания со стационарной амплитудой и с неизменной частотой.
Условие аэродинамической неустойчивости тела в потоке жидкости может быть записано в виде
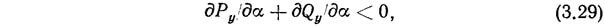
где
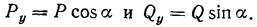
Для тел, обращенных плоской стороной к потоку, необходимо численными методами решать вопрос об устойчивости тела, используя графики cx=f1(?) и cy=f2(?), полученные опытным путем. Аэродинамически неустойчивые формы тел приведены в табл. 3.11. Они характерны отрицательным знаком производной дcy/д? в окрестности угла ?=90°.

Положение бесконечно длинной пластинки при углах атаки в окрестности 45° устойчиво, потому что дcy/д?>0. Это видно на рис. 3.7.
Строго говоря, чисто изгибные, поперечные к потоку, колебания упругих тел следует рассматривать как вырожденные изгибно-крутильные. Только поперечные к потоку колебания тел не наблюдаются, всегда будут кручение и движение в направлении оси х.
В обеспечении условий для возникновения колебаний роль крутильных колебаний, связанных с изгибными, очень велика. При определенных свойствах профиля именно они увеличивают углы атаки до таких значений, при которых возрастающая подъемная сила в направлении движения становится достаточной для покрытия потерь в колеблющейся системе.
Рассмотренная схема колебаний пластинки относится к идеализированному случаю отсутствия механических потерь. Поэтому условие (3.29) необходимо для возникновения колебаний, т. е. оно свидетельствует о возможной неустойчивости и необходимости дополнительного исследования для суждения о поведении системы.
В более общем виде формула (3.29) имеет вид

где D — рассеяние энергии в жидкости, в материале, узловых и опорных соединениях конструкции, в фундаментах и грунте, а также в демпфирующих устройствах.
При таком анализе полагают, что область неустойчивости системы ограничивается максимальной скоростью ветра, возможной в рассматриваемом географическом пункте.
Для пластинок наибольшее (результирующее, полное) аэродинамическое сопротивление будет при углах атаки ??90° (см. рис. 3.19), например, для плоской квадратной пластинки при угле ??38°. Характерно, что при дальнейшем увеличении угла атаки полное сопротивление пластинки резко падает, что приводит к неустойчивости, т. е. к изгибно-крутильным колебаниям. В строительстве такие колебания будут наблюдаться у плоских и криволинейных сплошностенчатых конструкций при косом ветре. Подобные колебания крыльев самолета называют срывным флаттером.
Поведение упругой пластинки в окрестности угла ?=0° существенно отличается от ее поведения при угле ?=90°. Предположим, что под влиянием небольшого изменения направления скорости потока пластинка повернулась на небольшой угол (см. рис. 3.50). Далее, если ничто не будет ей препятствовать, она будет поворачиваться до тех пор, пока угол а не станет равным 90°. Поворот пластинки будет сопровождаться появлением подъемной и восстанавливающей сил. В результате этого пластинка станет изгибаться и скручиваться с частотами, зависящими от ее динамических параметров. Эти связанные колебания, в общем случае неотделимые друг от друга, могут с известными допущениями вырождаться только в изгибные или крутильные.
Типичными примерами таких изгибно-крутильных колебаний могут быть висячие мосты и конструкции, имеющие форму двутавра, швеллера и более сложные формы (см. табл. 3.11). Решетчатые конструкции с горизонтальным настилом могут быть также аэродинамически неустойчивы. Такие формы сечения неустойчивы, если не считаться с изгибными и крутильными жесткостями и потерями энергии в конструкциях. В действительности при одинаковой форме и размерах поперечного сечения большепролетный мост может быть неустойчив, а мост небольшого пролета устойчив. Окончательное заключение об устойчивости сооружения может быть сделано лишь в результате исследования моделей в аэродинамической трубе и при обязательном учете рассеяния энергии.
При сильном порывистом ветре наблюдаются колебания обледенелых проводов и канатов с малыми частотами, но с амплитудами, измеряемыми метрами. Такое явление называют «пляской» или «галопированием». Опасность его заключается в отсутствии пока надежных средств гашения такого рода вибрации. Механизм таких колебаний заключается в следующем: вследствие обледенения цилиндра он принимает такую форму поперечного сечения, когда возникает явная подъемная сила, стремящаяся поддерживать и усиливать начавшиеся от случайного толчка колебания, т. е. удовлетворяется условие (3.30). Такие изгибно-крутильные колебания, типа флаттера крыла самолета, подобны колебаниям каната с профилем плоской пластинки в окрестностях угла атаки ?=0° у опорных закреплений.
Одностороннее обледенение труб, часто наблюдаемое в горных местностях, приводит их к неустойчивости.
При исследовании аэродинамической устойчивости сооружений предварительную оценку можно сделать по результатам опытов: по распределению давления по поверхности модели, по аэродинамическим коэффициентам сил и моментов их в функции угла атаки, определенным весовым способом, по поведению упруго подвешенной модели в потоке. Теоретическим путем пока невозможно дать заключение об аэродинамической устойчивости сооружения ввиду сложности анализа и недостаточности натурных и опытных данных. Чаще всего предлагаются полуэмпирические формулы — критерии устойчивости, справедливые, строго говоря, только для определенных типов, размеров и частот колебаний конструкции. Много еще неясного в рассеянии энергии при колебании сложных конструкций.
Недорогие исследования моделей сооружения или его отсеков могут внести ясность в поведение конструкции при ветре, заставить принять .необходимые меры и тем предотвратить нежелательные явления, ликвидация последствий которых обходится во много раз дороже.