В процессе компоновки схемы моста и на дальнейших этапах его проектирования устанавливают пологость арок, очертание их оси, конструкцию арок и балок жесткости, (сплошные или сквозные), форму, тип и высоту сечения арок и балок жесткости, число арок и балок жесткости.
Пологость арок в мостах с ездой поверху в большинстве случаев ограничена отметкой профиля дороги, горизонтом высоких вод и ледохода и подмостовым габаритом. В мостах с ездой посередине и понизу, а в отдельных случаях и при езде поверху, открывается возможность варьировать пологость арок в весьма широких пределах.
Вес арок определяется их длиной и необходимыми размерами поперечных сечений, которые зависят от величины расчетных усилий — продольной силы и Изгибающего момента. Подсчеты веса арок моста пролетом 100 м под однопутную железную дорогу показывают, что минимальный вес арок соответствует пологости их примерно в 1/5. Если этот вес принять за 100%, то веса арок при иных пологостях составят: при пологости 1:1,5 — 107%, при пологости 1:10 — 103%, при пологости 1:15 — 113,5%.
Пологость в 1/5 вполне приемлема и в эстетическом отношении. Вообще же пологие арки выглядят лучше крутых. Решая вопрос о влиянии пологости на общую стоимость моста, необходимо учитывать удорожание опор в вариантах с более пологими арками в распорных системах. Увеличение размеров опор в значительной мере зависит от местных геологических условий.
Очертание оси арок при заданных пролете и стреле выбирается таким, чтобы расчетные моменты в сечениях арки были по абсолютной величине возможно меньшими. Возникновение изгибающих моментов в арке является результатом несовпадения оси арки с кривой давления, которая меняет очертание при каждом изменении положения временной нагрузки на арке. В статически неопределимых арках неизбежно возникновение изгибающих моментов от упругого обжатия арки и изменения ее температуры. Можно лишь стремиться к тому, чтобы неизбежные отклонения кривых давления от оси арки были наименьшими.
При нагрузке, равномерно распределенной по всему пролету арки, очертание кривой давления будет, как известно, квадратной параболой. В металлических арочных мостах, особенно городских (с тяжелой проезжей частью), действительное распределение постоянной нагрузки по длине пролета весьма близко к равномерному, поэтому очертание оси арок обычно назначают по квадратной параболе.
Недостатком квадратной параболы как оси арки является ее переменная кривизна, препятствующая унификации узловых сопряжений, а в сквозных арках также унификации длин элементов решетки. В этом отношении более удобна круговая кривая. Из этих соображений она была принята для осей арок в ряде проектов арочных и комбинированных мостов советской проектировки. В то же время круговая кривая по сравнению с квадратной параболой менее рациональна в отношении величины расчетных изгибающих моментов; применение ее для очертания осей арок приводит к некоторому утяжелению арок, которое тем заметнее, чем больше отличается круговая кривая от параболы, т. е. чем подъемистее арка. Выгодность выбора того или иного решения определяется стоимостью пролетного строения, которая слагается из стоимости металла и стоимости заводского изготовления.
Высота арки является основным размером ее поперечного сечения, от которого зависят вес арки и ее жесткость. Жесткость арки определяет, в свою очередь, величину возникающих в ней моментов от изменения температуры.
Для сплошных жестких арок так же, как и для балок, существует наивыгоднейшая высота, при которой вес арки получается наименьшим. Для железнодорожных мостов эта высота составляет примерно 1/40 пролета; для автодорожных и городских мостов — 1/50—1/70.
Однако отступление от наивыгоднейшей высоты в сторону увеличения или уменьшения сказывается на весе арки сравнительно мало. Так, изменение высоты арки по сравнению с наивыгоднейшей на 20% вызывает утяжеление ее веса на 3—5%. Это дает возможность в известных пределах подчинить высоту арки эстетическим требованиям или удобствам заводского изготовления и перевозки без существенных потерь в расходе металла для изготовления арок.
Минимально допустимая высота арок определяется требованиями жесткости.
По СН 200-62 (п. 52) требуется, чтобы сумма максимальных абсолютных значений прогибов разных знаков, отвечающая одному положению временной вертикальной нагрузки, не превосходила 1/800 расчетного пролета для железнодорожных, 1/400 l для городских и автодорожных мостов на дорогах I—IV категорий и 1/300 l на дорогах V категории.
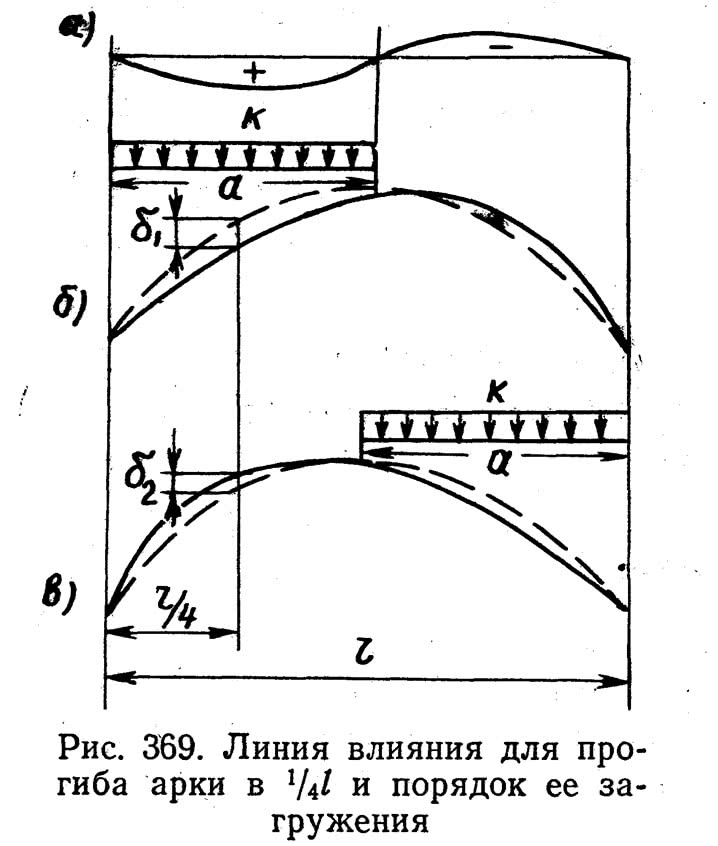
Выполнение требований жесткости проверяют обычно при загружении временной вертикальной нагрузкой половины пролета и вычислении прогибов в четвертях пролета.
В ряде городских мостов с пологими арками, сооруженных в 30-х годах через р. Москву, отношение высоты арок к пролету близко к 1/60.
Стенки сплошных арок делают обычно большей толщины, чем стенки балок той же высоты. Хотя при работе на момент материал поясов используется лучше, чем материал стенок, наличие в арках нормальной силы вынуждает (для обеспечения устойчивости стенок) увеличивать отношение их толщины к высоте.
В арках двутаврового профиля это отношение не превышает 1/60; в коробчатых арках, пояса которых лучше удерживают стенки от поворота при выпучивании из плоскости стенок, отношение толщины стенок к высоте берут чаще всего в пределах 1/60?1/100.
Близость по величине положительных и отрицательных моментов в сечениях арки обеспечивает хорошее использование материала в обоих поясах арки при сечении арки, симметричном относительно горизонтальной оси.
В пологих арках (при f/l?1/5) влияние упругого обжатия арки приводит к преобладанию изгибающих моментов одного знака над изгибающими моментами другого знака.
В двухшарнирных арках во всех еечениях преобладают положительные моменты; в бесшарнирных арках в средней части арок преобладают положительные моменты, в концевых частях — отрицательные моменты.
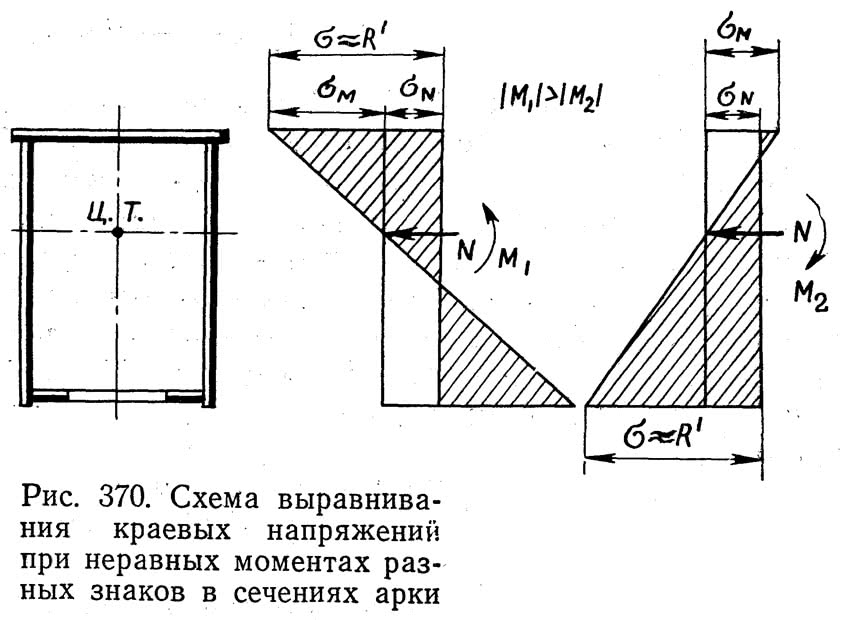
Существенное преобладание момента одного знака над моментом другого знака делает экономичным применение несимметричных сечений. Преобладание положительного момента требует более мощного сечения верхнего пояса (рис. 370) и наоборот.
Все сказанное выше о проектировании арок относится ж аркам, работающим на сжатие с изгибом, независимо от того, с какой системой мы имеем дело: с арочной или комбинированной. Несколько иное положение наблюдается при проектировании гибких арок и балок жесткости в комбинированных системах.
Гибкая арка, являющаяся по существу уже не аркой, а стержневым многоугольником, работает в предположении шарнирности узловых сочленений на центральное сжатие. Свободную длину отдельных стержней многоугольника при наличии между ними продольных связей принимают в вертикальной плоскости равной геометрической длине стержней, а в плоскости связей — расстоянию между узлами связей. При равной свободной длине в обеих плоскостях сечение стержней может быть подобрано с близкими по величине моментами инерции относительно обеих главных осей. Наиболее удобной формой поперечного сечения стержней является Н-образная форма, так как при этой форме сечения стыки полок, в которых размещена основная площадь сечений, могут быть перекрыты плоскими (не требующими выгиба) накладками.
Наиболее целесообразным сечением балки жесткости является двутавровое сечение. Толщину стенки балки выгодно делать минимальной, доводя отношение ?/h до 1/200 и даже менее.
Высота балки должна удовлетворять требованиям жесткости пролетного строения. В системах, имеющих при загружении половины пролета S-образный прогиб, высоту балки обычно приходится назначать по условиям жесткости пролетного строения. Предварительную довольно точную оценку этой жесткости можно получить по формуле:
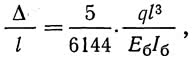
где ? — сумма абсолютных значений наибольших расчетных прогибов обоих знаков в четверти пролета от статической временной вертикальной нагрузки q, установленной на протяжении полупролета; l — пролет; Eб и Iб — модуль упругости и осредненный момент инерции брутто балки жесткости.
Отношение ?/l нормируется для балок жесткости так же, как для арок.
В существующих мостах отношение высоты балки жесткости к пролету принимают 1/25?1/35 для железнодорожных мостов и 1/40?1/50 для автодорожных мостов.