Геометрические построения
В процессе граверных работ довольно часто приходится производить разметку некоторых геометрических фигур. Для этого необходимо усвоить простые геометрические построения, практикуясь сначала на бумаге.
Разметка заготовок. Для симметричного расположения текстов и других изображений на заготовках надо разделить прямую на два или несколько равных отрезков.
Чтобы разделить отрезок АВ (рис. 8, а) пополам, нужно ножку циркуля поставить в точку А и радиусом, несколько б?льшим половины длины прямой, провести дугу. Затем тем же радиусом из точки В сделать засечки на дуге в точках С и D. Прямая линия, соединяющая точки С и D, перпендикулярная отрезку АВ, пересечет его в точке О и разделит на два равных отрезка АО и ОВ. Таким же образом можно разделить пополам отрезки АО и ОВ и т. д.
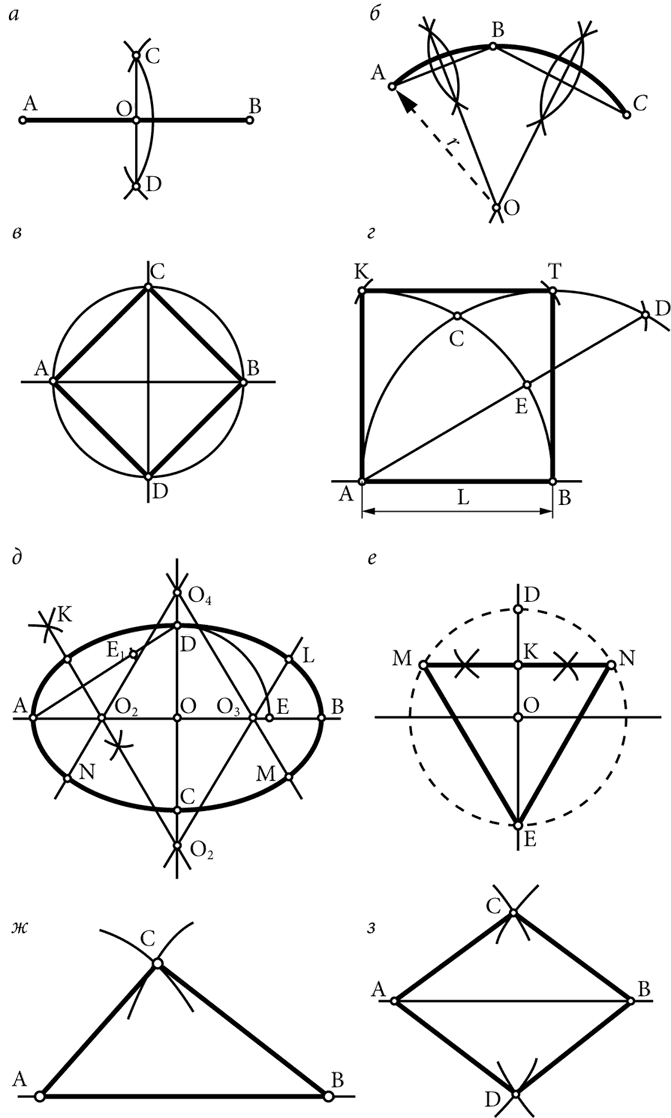
Рис. 8.
Нахождение центра и радиуса дуги. Иногда в граверной практике применяют дугообразные заготовки, на которые необходимо нанести угловые деления, а центр, нужный для точной установки таких заготовок, не всегда известен. Определение центра также бывает необходимым и для других геометрических построений. Для нахождения центра и определения длины радиуса любой дуги применяют следующий способ. На заданной дуге отмечают три произвольные точки А, B и С и соединяют их прямыми (рис. 8, б). Делят отрезки AB и CB пополам и через их середину проводят взаимные перпендикуляры до их пересечения в точке О, которая и будет центром дуги. Расстояние r от точки О до дуги будет искомым радиусом.
Построение квадрата. Построить квадрат несложно, но иногда его размещение обусловлено рядом дополнительных условий. Для построения квадрата в таких случаях существует несколько способов. Рассмотрим два из них, наиболее простые.
Первый способ: сторона квадрата не обусловливается определенным размером (рис. 8, в). Для построения такого квадрата прежде всего следует вычертить окружность произвольного радиуса. Точки пересечения окружности с двумя взаимно перпендикулярными диаметрами (A, C, B и D) соединяют прямыми, в результате чего получается квадрат, диагонали которого равны диаметру окружности.
Второй способ – построение квадрата со стороной заданной длины (рис. 8, г). На произвольно взятой прямой откладывают отрезок АВ, равный заданной длине L. Из точек А и В проводят дуги радиусом, равным заданной длине, которые пересекутся в точке С. Из точки С тем же радиусом делают засечку на продолжение дуги AC и получают точку D. Соединяют точку D с точкой А прямой, которая пересечет дугу ВС в точке Е. Из точки С радиусом, равным CE, делают засечки на продолжении дуг (в верхней части) AC и BC и получают точки К и Т. Соединив точки А и К, К и Т, Т и В прямыми линиями, получают квадрат требуемого размера.
Построение эллипсов. Если заданы значения горизонтальной АВ и вертикальной CD осей (рис. 8, д), то построение эллипса производят следующим образом. Начертив перпендикулярные прямые, от точки О откладывают на них полуоси. Из точки О радиусом OD проводят дугу вправо до пересечения с горизонтальной осью в точке Е. Затем проводят прямую AD, на ней от точки D откладывают отрезок, равный BE (разность между горизонтальной и вертикальной полуосями) и получают точку Е1. К середине отрезка прямой АЕ1 восстанавливают перпендикуляр и продолжают его до пересечения с горизонтальной полуосью в точке О1 и вертикальной полуосью в точке O2. Величину отрезка О1О откладывают вправо от точки О на горизонтальной оси и получают точку О3, а величину отрезка ОО2 откладывают вверх от точки О на вертикальной оси и получают точку О4. Точки О1 и О3 являются центрами концевых дуг, а точки О2 и О4 – центрами верхней и нижней серединных дуг эллипса. Радиусами концевых дуг будут отрезки О1А и О3В, а радиусами верхней и нижней серединных дуг будут отрезки О2D и О4С. Построив все четыре дуги, сопряженные в точках К, L, М и N, получают эллипс.
Построение треугольников. Для построения правильного треугольника, вписанного в окружность (рис. 8, е), надо разделить радиус OD пополам и точки пересечения М и N линии деления с окружностью соединить хордами с точкой Е, в результате чего получится равносторонний треугольник EMN.
Если даны размеры всех трех сторон треугольника, то построение треугольника с заданными размерами сторон происходит так. Отложив на прямой одну из сторон АВ треугольника (рис. 8, ж), растворами циркуля, равными последовательно длинам двух других сторон, проводят дуги из концов прямой АВ. Точка пересечения С будет вершиной треугольника. После проведения линий AC и СВ получится заданный треугольник.
Построение ромба. Если даны стороны ромба и его большая диагональ, то ромб можно построить следующим образом. На прямой откладывают величину большой диагонали АВ (рис. 8, з), затем, поставив ножку циркуля в точку А, описывают дуги радиусом, равным стороне ромба, над линией АВ и под ней. То же делают и из точки В. Дуги пересекутся в точках С и D. Соединив точки A, С, В и D, получают ромб.



